传统区块链能够将数据以链式结构存储在一起, 且保证数据真实和不可篡改. 在公共平台中, 区块链的这一重要属性只能通过分散的经济机制(如工作证明(Pow))来实现. 然而, 传统区块链的这一特性也带来了很显著的缺点. 自从国际刑警组织揭露比特币区块链中存在有害和潜在的非法文档、图像和链接以来, 学者在分析比特币区块链中已有的数据进行了许多工作. 随着监管政策和政府法律的改变, 人们开始着眼于优化比特币的这一特性, 使其在某些特定条件下可以进行修改或者删除部分不合理的内容, 并保证区块链的安全可信的性质. 本文介绍了几种近几年学术界提出的可编辑区块链方案, 并对其实现原理、操作类型、编辑粒度等方面进行了分析.
区块链是以比特币为代表的数字加密货币的核心支撑技术, 是一种全新的去中心化基础架构与分布式计算范式[1]. 区块链的技术特点可以归纳为“TRUE”和“DAO”, 前者表示可信(Trustable)、可靠(Reliable)、可用(Usable)和高效(Effective,efficient), 其中高效指的是区块链技术将带来社会运行效率的提高; 而后者则表示分布式与去中心化(Distributed,decentralized)、自主性与自动化(Autonomous,automated)、组织化和有序性(Organized,ordered)[2].
现有的区块链系统中, 数据一旦上链便无法更改. 随着区块链的发展, 区块链已不仅仅局限于金融领域, 大量的数据被记录到区块链上, 使得修改区块链上的错误数据、删除非法信息的需求日渐突出. 因此, 区块链相关研究和应用实践正呈现出从“乌托邦”回归现实的趋势[3]. 为了使区块链应用到更加广阔的领域, 我们不得不放弃区块链不可更改这一特性, 但我们放弃的程度也是有限的, 只有达到某种共识时, 才可对区块链进行修改.
引言
区块链是一种按照时间顺序将数据以链的形式存储的分布式记账系统. 传统的分布式数据库需要一个中心服务器进行数据维护. 而在区块链中每个节点都有完整的数据备份, 且每个节点都扮演着“中心节点”的角色, 数据的维护由所有节点基于共识机制共同完成. 对某个节点的攻击并不会影响区块链系统的正常允许, 因此区块链具有更好的安全性和可靠性.
随着区块链的快速发展, 学术和工业领域通常将区块链按照开放程度分为三类[12], 分别是公有链、联盟链和私有链. 三种区块链对比如下表.
| \textbf{公有链} | \textbf{联盟链} | \textbf{私有链} | |
|---|---|---|---|
| 中心化程度 | 完全去中心化 | 半中心化 | 中心化 |
| 参与者 | 所有人 | 联盟授权用户 | 指定用户 |
| 共识机制 | Pow/Pos/DPos | BPFT | BPFT |
| 记账人 | 所有用户 | 授权节点 | 自定义 |
| 例子 | BTC、ETH | R3联盟 | Multichain |
对于传统区块链来说, 区块链的完整性验证保证了区块链的不可篡改性. 区块链中每一区块的头部哈希保证了区块链的链向的完整性, 而Merkle树保证了区块链每一区块内数据的完整性. 因此, 从这两个验证关系入手, 可以实现可编辑区块链的设计.
加密原语
基本的区块链模型
基于现有文献[4], 本文将采用如下区块链模型: 假设区块链$C_N$ 是首尾相连的区块组成的单条链, 其中$N$为最新区块的高度, 仅包含创世区块的$C_1$高度为1; 每个区块记为三元组$B_i=\langle{s_i,x_i,ctr_i}\rangle,i\in[0,N]$, $B_0$和$B_N$分别为创世区块和最新区块. 三元组中, $s_i\in\{0,1\}^K$是 位的前一区块的哈希值, $x_i\in\{0,1\}^*$是任意长度的数据,$ctr_i\in N$ 是当前区块共识过程中生成的随机数Nonce. 由此, 下一区块的相关数据与本区块之间满足$S_{N+1}=H(ctr_N,G(s_N,x_N))$, 其中$H:\{0,1\}^*\rightarrow\{0,1\}^K$和$G:\{0,1\}^*\rightarrow\{0,1\}^K$为$K$位的抗碰撞哈希函数, 分别为外哈希函数和内哈希函数. 为保证区块链的有效性和完整性, 以下两式必须成立:
$$ \begin{aligned} Valid^D_q(B_i)&=(H(ctr_i,G(s_i,x_i))< D)\cap(ctr_i<q)=1 \\ s_{i+1}&=H(ctr_i,G(s_i,x_i)) \end{aligned} $$
其中, 参数$D\in N$是当前区块链的难度,$q$是每一轮共识过程中最大允许的哈希请求数. 此外, 本文中, 我们用$C_\empty$表示空链, $C^{[k}$表示去掉较新的$k$个区块后的区块链, 而$C^{k]}$表示去掉历史上较旧的$k$个区块后的区块链.
变色龙哈希函数
变色龙哈希函数是一种特殊的哈希函数, 它可以有效地利用陷门密钥生成哈希碰撞\upcite{5}. 考虑消息$m$和随机选择的参数$r$. 给定一个陷门密钥$tk$, 持有陷门密钥的人可以使用变色龙哈希函数找到一对$(m,r)$和$(m^\prime,r^\prime)$, 使得$CH(m,r)=CH(m^\prime,r^\prime)$, 其中$CH()$表示变色龙哈希函数. 注意, 消息$m$和$m^\prime$应当是不同的, 即$m\neq m^\prime$.
一个标准的变色龙哈希函数包括以下高效(多项式时间)算法: 密钥生成($HG$)、哈希计算($H$)、哈希验证($HV$)、哈希碰撞($HC$).
密钥生成算法
$HG(1^n)=(hk,tk)$: 使用$n\in N$作为安全参数输入, 生成变色龙哈希函数的公钥$hk$和陷门私钥$tk$.
哈希计算算法
$H(hk,m;r)=(h,z)$: 使用公钥$hk$, 消息$m$和随机数$r$作为输入, 生成对$(h,z)$. 其中$h$为哈希值, $z$为校验字符串.
哈希验证算法
$D=HV(hk,m,(h,z))$: 使用消息$m\in M$, 公钥$hk$, 哈希值$h$和校验字符串$z$为输入, 输出一比特$D$, 如果$(h,z)$是消息 的有效哈希对, 则$D$等于1, 否则等于0.
哈希碰撞算法
$C=HC(t,(h,m,z),m^\prime)$: 使用陷门密钥$tk$, 一个有效元组$(h,m,z)$和新消息$m^\prime$作为输入, 输出一个新的校验字符串$z^\prime$满足:
$$ HV(hk,m,(h,z))=HV(hk,m^\prime,(h,z^\prime))=1 $$
秘密共享
秘密共享[6]是一种面向组的加密方法, 可以将机密信息的知识从单个实体转移到一组实体, 可以用来实现陷门密钥在多个验证者之间的安全共享. 披露机密信息需要满足特定条件. Shamir[7]的阈值方案基于多项式插值, 允许$n$个参与者中的任意$k$个参与者恢复机密信息. 将机密信息 随机分成$n$份, 且须满足以下两个条件:
- 利用其中的$k$个或更多的子份额可以很容易的重建机密信息
- 任何小于$k$个的子份额都无法重建机密信息
此方案称为$(k,n)$阈值方案. 如果$k=n$, 则每个共享机密信息的参与者都需参与重建机密信息 . 此方案由如下两个算法组成:
- 秘密分发算法$Share(tk)=(\tau_1,\tau_2,...,\tau_N)$: 给定陷门密钥$tk$, 随机生成$n$个份额$(\tau_1,\tau_2,...,\tau_N)$;
- 秘密恢复算法$Rec(\tau_1,\tau_2,...,\tau_N)=tk\lor\perp$: 给定$n$个份额$(\tau_1,\tau_2,...,\tau_N)$, 恢复陷门密钥$tk$ 或者返回异常值$\perp$.
![$(k,n)$秘密共享方案[9]](https://blog.gaoruixiao.com/usr/uploads/20210129190402.png)
Sharmir的秘密共享方案是一种线性秘密共享(LSS)方案, 存在大量漏洞, 但我们可以使用其他非线性秘密共享方案来管理密钥. 利用秘密共享方案管理陷门密钥可以避免恶意攻击者获得陷门后随意篡改数据, 从而提高区块链的安全性和可信度.
安全多方计算
多方计算(MPC)是一种当事各方通过私有输入共同计算函数的方法\upcite{8}. 私有输入可以通过秘密共享方案中得到. 考虑一个多方计算, $n$个用户$u_1,u_2,...,u_n$对应输入数据为$d_1,d_2,...,d_n$. 所有的用户使用公开函数$f$ 在他们的输入上进行计算并保证各自输入的保密性:$f(d_1,d_2,...,d_n)$.
取决于计算过程有无可信第三方,常见安全多方计算情景可以分为两种典型情形:
- 存在可信第三方, 参与运算的各方将数据发送给可信第三方, 由第三方进行运算, 并给出结果.
- 不存在可信第三方, 参与运算的各方通过某一算法参与运算, 得出最终结果并保持自己输入的机密性.
数字签名
数字签名是一种基于数学运算的证明数字文档真实性的方案[10]. 数字签名得益于身份验证、不可否认性和完整性等特点, 被广泛应用于各行各业. 一个典型的数字签名方案通常包括3个阶段, 即密钥生成($G$)、签名($S$)和签名验证($V$).
密钥生成: 使用$r\in N$做为安全参数, 输入为$1^r$, 输出公钥$pk$和私钥$sk$
$$ (pk,sk)\leftarrow G(1^r) $$
签名: 使用私钥$sk$, 消息$m$作为输入, 输出签名$t$
$$ t\leftarrow S(sk,m) $$
签名验证: 使用消息$m$, 公钥$pk$和签名$t$作为输入, 如果$t$是$m$的签名, 输出$D=0$, 否则输出$D=1$
$$ D\leftarrow V(pk,m,t) $$
区块级的单链的可编辑区块链算法
2017年, Atenises等[4]最早提出基于变色龙哈希函数的区块链修改方案, 在已知陷门时, 可以对区块数据进行修改, 这一方案具有兼容性强、适合目前主流的区块链架构等优良特点, 特别对具有少数可信验证者的授权区块链来说尤其适用. 但在该方案中, 陷门被交与1个或多个可信中心, 修改权被中心化, 极大威胁了区块链的安全性和可靠性. Li等[11]人对可编辑区块链技术进行了改进, 适用秘密共享方案, 将陷门分配给区块链系统中的多个节点, 并设置恢复阈值, 只有当同意修改区块链的节点数达到阈值时, 才对区块链进行编辑. 但该方案的修改粒度是区块, 修改指定交易需要对交易所在的整个区块进行修改, 粒度太大, 且在公开链上, 当参与秘密共享的节点数较大(超过200)时性能较差. 此外, 该系统还会留下一个不可变的“疤痕”来来指示何时修改了哪个区块, 从而保持了可审计性和透明度[17].
私有链实现
上文提到私有链是中心化的区块链, 假设存在唯一的中心化验证者, 算法的主要目的就是让该验证者拥有陷门密钥并可以进行区块链的修改. 算法的主要思想就是将上文中提到的内哈希函数(即函数$G$)改用变色龙哈希函数. 直观地, 通过查找变色龙哈希函数的冲突(无需修改外部哈希函数), 便可以重新编辑每个块的内容$x$.
区块链定义
将之前的定义进行简单的修改, 以使区块链更好地工作. 区块$B_i$现在是一个元组$B_i=\langle s_i,x_i,ctr_i,(h_i,z_i)\rangle$, 其中$s_i,x_i,ctr_i$和之前定义相同, $(h_i,z_i)$是变色龙哈希的哈希/检查对. 函数$G$被定义为变色龙哈希$CH=(HG,Hash,HV,HC)$. 此时保证区块链完整性的要求为:
$$ Valid^D_q(B_i)=(H(ctr_i,h_i)<D)\cap(HV(hk,(s_i,x_i),(h_i,z_i)))\cap(ctr_i<q)=1 $$
给定链$C_N$与链头$B_N=\langle s_N,x_N,ctr_N,(h_N,z_N)\rangle$, 可以通过附加一个有效块$B_{N+1}$将其扩展到链$C_{N+1}$, 其中$B_{N+1}=\langle s_{N+1},x_{N+1},ctr_{N+1},(h_{N+1},z_{N+1})\rangle$且$s_{N+1}=H(ctr_N,h_N)$.
为了减少存储, 哈希值$h$和验证值$z$是不需要存储的, 因为哈希值可以通过变色龙哈希函数的输入和随机数确定. 这样, 区块$B_i=\langle s_i,x_i,ctr_i,r_i\rangle$, 其中$r_i$是第区块$B_i$中变色龙哈希函数取得随机值.此时保证区块链完整性的要求为:
$$ Valid^D_q(B_i)=(H(ctr_i,Hash(hk,(s_i,x_i);r_i))<D)\cap(ctr_i<q)=1 $$
这样, 给定$C_N$与链头$B_N$可以通过附加有效区块$B_{N+1}$扩展区块链, $s_{N+1}=H(ctr_N,Hash(hk,(s_N,x_N);r_N))$.
编辑区块
当前模型下编辑区块的算法如算法1所示, 该算法以链$C$, 要编辑的区块索引, 以及要编辑的区块内部修改后的数据, 带着变色龙哈希函数陷门密钥$tk$作为输入, 输出完成修改后的链. 当得到修改后的链时, 验证者应该广播这个链, 并让其他节点采用新链.

删除区块
可编辑区块链的另一可能性是将整个块从链中完全删除. 算法如算法\ref{alg:2}所示, 为了删除区块$B_i$, 需要将$B_{i+1}$的$s_{i+1}$修改为$s_i$, 并计算新的$B_{i+1}^\prime$保持链的完整性. 和算法1一样, 得到结果后, 验证者应将新链广播并让其它节点接收新链, 并在新的链上继续工作.

公有链或联盟链实现
对于多中心或去中心化的区块链来说, 可以通过秘密共享技术将陷门密钥安全地分发给预定义的验证者集合. 当需要修改链上的数据时, 启动安全多方计算, 进行分布式计算, 从而实现修改链上数据的操作.
区块链定义
同上
编辑、删除区块
当块$B:=\langle s,x,ctr,(h,z)\rangle$ 需要被修改为$B^\prime:=\langle s,x^\prime,ctr,(h,z^\prime)\rangle$, 每个验证者都需要检查自己的区块链并找到区块$B$. 之后, 每个验证者需要以分布式方式执行算法1. 特别的, 每个验证者将自己的$\tau_i$作为输入参与多方计算出陷门密钥$tk$, 为了获得修改值$z^\prime$需要在公共输入$((H,s||x,z),s||x^\prime)$上执行哈希碰撞函数$HC$.
算法2的修改和上述过程类似, 采用安全多方计算即可.
陷门密钥管理
在之前的叙述中已经简单的介绍了陷门密钥的管理, 这里总结一下.
私有链
此类区块链广泛应用于金融领域[13], 仅中心节点被授予写入权限, 读取权限可能公开也可能受限. 这种情况下, 陷门密钥只需交给中心节点管理即可.
联盟链
在这种类型的区块链中, 通常由一组实体达成共识. 在这种情况下, 陷门密钥可以在联盟体的所有各方共享, 并使用安全多方计算进行链的修改.
公有链
在这种类型的区块链中, 参与其中的节点都可以将交易发送到网络, 并在交易合法的情况下记录到区块链中. 在这种情况下, 有两种方案来管理陷门密钥:
- 陷门密钥可以分布在网络的所有节点之间. 当网络中的参与多方计算的阈值较高时, 由于多方计算协议的性能问题, 效率可能比较低.
- 陷门密钥可以分布在精心挑选的节点子集中, 例如挖矿哈希速率最高的几个节点. 尽管这也是某种程度上的中心集权, 但此方案不会改变现有的信任假设.
交易级的单链可编辑区块链算法
Puddu[14]方案提出可变交易(Mutable transactions)概念, 通过修改区块交易结构, 使得用户和验证者可以在交易上链后的某个时刻以追加发布新交易的方式扩展旧交易, 从而实现交易级单链的追加修改.
可变交易
可变交易表示为三元组$(T,a,P)$, 其中$T$为交易集, $a$确定活动的交易, $P$指定变更策略. 交易集包括多个交易, 其中每个交易对应于一个可能的交易版本. 特别的, 交易集$T$定义为$T=(\tau_1,...,\tau_k)$, 其中任意$\tau_i\in T$可能有以下三种类型:
- 标准交易(Classical): 这些是由特定发送方$S$签名给指定接收者$R$的传统交易, 将一定数量的加密货币从$S$传输到$R$, 还可以包含一个数据字段.
- 合约交易(Deploying): 这种类型的交易用于在区块链上部署智能合约. 发送者$S$签名交易并发送到所有的验证器. 在数据字段中通常包含要部署的代码.
- 空交易(Nope): 这些是没有发送方、接收方以及数据字段为空的交易.
任何可变交易至少包含一个标准交易或者合约交易, 并且在交易集中包含一个空交易. 此外, 同一交易集中的所有标准交易与合约交易必须具有相同的发送方$S$和接收方$R$\footnote{这表示同一交易集中不能同时出现标准交易与合约交易, 因为两者的接收者不同.}.
发送者$S$指定交易集$T$中的$\tau_a$为默认的活动交易. 变更策略$P$定义了更改活动交易的条件. 特别地, 策略$P$指定了谁被允许修改活动交易. 此外, 他还可以指定交易集在未来是可扩展的, 并指定谁被允许添加新的交易. 最后, 策略$P$还可以制定一个时间窗口$\Delta t$, 在这个时间窗口内, 交易集保持可变或可扩展, 超出时间窗口后变成不可变的和不可扩展的.
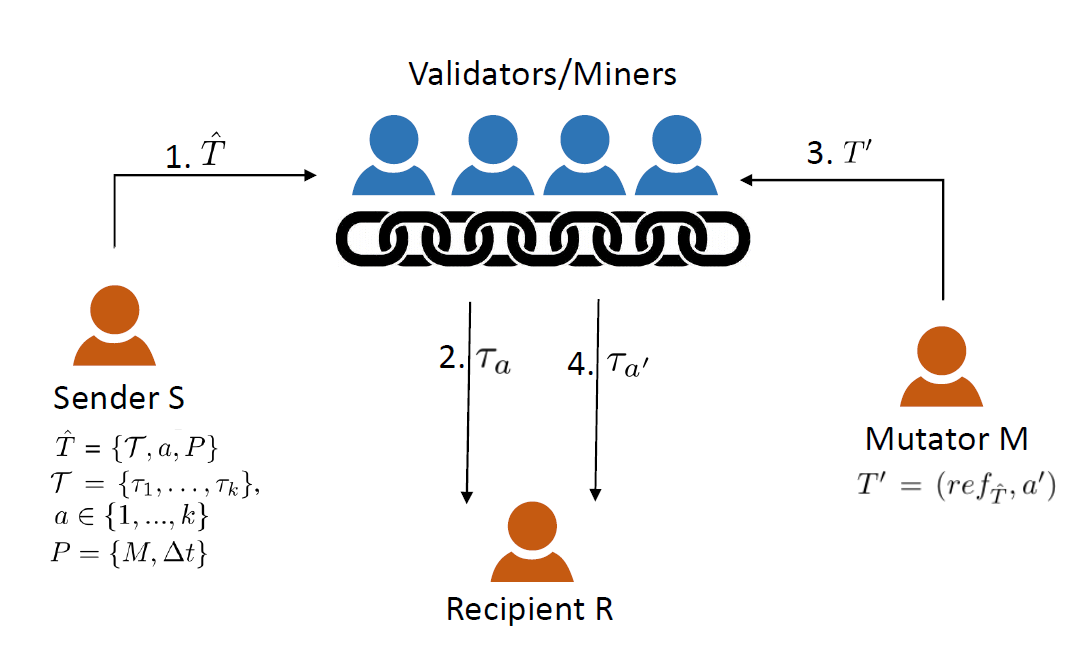
修改交易历史
通过发出一个特殊类型的交易, 即变更交易, 可以将默认事务$\tau_a$替换为任意的$\tau_{a^\prime}\in T$.
- 变更(Mutant): 这是一种新的交易类型, 类似于合约交易, 它有一个发送者, 但没有特定的接收者, 并被隐式地发送给区块链中所有的验证器. 变更交易指定可变交易$T$, 以及新的活跃交易$\tau_{a^\prime}$. 变更交易需要由发送发签名, 并且只能由变更策略$P$中指定的合法方发送.
基于上述交易结构与交易逻辑的改进, 算法3和图2给出了区块链数据修改的简要步骤.
![图1: 基于可变交易的区块链修改流程[14]](https://blog.gaoruixiao.com/usr/uploads/20210129191626.png)
从上述算法中可以看出, Puddu 方案并不物理修改区块链上的数据, 只是指定区块中的活跃(有效)交易, 旧的活跃交易并不会被修改或删除. 这样, 区块的哈希并不会发生改变, 因此也不会改变哈希链路的完整性.
扩展交易集
申请扩展人$E$可以通过发送一类特殊的交易, 称为扩展交易, 来扩充一个可变交易$T$.
- 扩展(Extending): 这是一种新的交易类型, 有发送方, 但没有特定接收方. 扩展交易指定一个可变交易$T$ 和一个扩展集合$T_x={\tau_{k+1},...,\tau_m}$, 其中包含$m-k$个新的交易备选项. 扩展交易需要由$P\in T$指定的合法申请扩展人发送并需要其进行签名. 此外, 所有的交易备选项$\tau_i, k<i\leq m$必须和$T$中的交易有相同的发送者$S$和接收者$R$.
扩展交易没有自己的策略, 当扩展交易被区块链接受时, 它将成为原可变交易的一个扩展. 此外, 扩展交易中也没有任何活跃的交易$\tau_x$, 可以通过发送变更交易将$T$中的活跃交易指定到扩展交易中的交易备选项上.
双区块链可编辑区块链算法
Marsalek等[15]提出了使用两条区块链的想法. 即使用其中一条链作为数据链保存原始数据, 另一条链以区块为粒度存储修改后的新数据.
区块链架构
可编辑区块链$C$由两条区块链组成, 其一为标准链$C_S$, 另一个为修正链$C_C$, 两个链都从同一个创世区块开始. 在$C_S$上的区块具有四元组形式$BS:=\langle ss,xs,ctrs,rs\rangle$, 其中$ss\in\{0,1\}^K, xs\in\{0,1\}^*,ctrs\in N, rs\in\{0,1\}^K$. 这里$ss$为$C_S$中上一个区块的哈希值, $xs$是$BS$的数据, $ctrs$代表PoW, $rs$是$C_C$中最后一个块的哈希值. 在$C_C$上的区块具有元组形式$BC:=\langle sc,xc,ctrc,H(E),H(BS_{i+1},H(BS_n))\rangle$, 其中$sc\in\{0,1\}^K, xc\in\{0,1\}^*,ctrc\in N$, 且$H(E),H(BS_{i+1},H(BS_n)\in\{0,1\}^K$.
这里$sc$是$C_C$中上一个区块的哈希值, $xc$是$BC$中的数据, $ctrc$代表PoW, $H(E)$是选举TX$E$的哈希值, $H(BS_{i+1})$是$BS_{i+1}$的哈希值. 选举TX$E:=\langle ss_i,G(xs_i),xs_i^*,ctrs_i,rs_i\rangle$包含块$BS_i$中除了数据$xs_i$外所有要更正的信息. 而哈希值$G(xs_i)$和新的修正过的数据$xs_i^*$都被包含在里面. 使用这个信息, 每个参与者都可以根据区块链策略$P$验证建议的更正是否被确认. 策略$P$指定允许的修改并指定是合法修改的条件.
定义标准链$C_S$上区块$BS$的哈希值为$H(BS):=H(ss,rs,G(xs,ctrs)$, $C_C$上区块$BC$的哈希值为$H(BC):=H(sc,G(xc),ctrc,H(E),H(BS_{i+1}),H(BS_n))$, 其中$H(E):=H(ss_i,G(xs_i),xs_i^*,ctrs,rs_i)$. 可以很简单的得出区块链$C$的增长过程, 此处不再赘述.
修改区块
为了修改区块$BS_i:=\langle ss_i,xs_i,ctrs_i,rs_i\rangle$, 需要执行以下几个步骤:
- 首先, 用户或者矿工创建并广播选举 TX$E:=\langle ss_i, G(xs_i),xs_i^*, ctrs_i, rs_i\rangle$, 其中$xs_i^*$是用来替代$xs_i$的数据.
- 然后选举 TX$E$存储到区块链的内存池中, 之后进入一个区块.
- 当$E$或$H(E)$进入区块后, 投票期开始. 每个矿工在每个矿区有一票, 这确保了区块链的信任假设保存不变.
- 投票期到期后, 如果大多数人支持提出的更正, 则下一个区块会变成修正块$BC$, 否则为标准块$BS$. 此时, 如果成功更正, 读取$C_S$时类似于用$E$中指定的虚拟块填充了删除块$BS_i$带来的空白.
![图3: 双区块链可编辑区块链更正示例[15]](https://blog.gaoruixiao.com/usr/uploads/20210129191844.png)
双哈希链可编辑区块链算法
与双区块链算法不同, 双哈希链模式[16]仅保留单条区块链, 通过修改区块结构使得区块链上存在两条哈希链路. 在修改区块时, 可以保持其中一条哈希链路不被破坏. 它的协议使用基于PoW的共识投票机制, 并在被区块链策略批准的情况下才会执行修改. 该方案的概念实现了在修改区块时, 链式验证中的增加了较小的开销, 并认为去中心化区块链中大部分矿工是诚实的[17].
区块链结构
区块链中区块$B$具有元组形式$B:=\langle s,x,ctr,y\rangle$, 其中$s\in\{0,1\}^k$为前一个区块的哈希值, $x\in\{0,1\}^*$为当前区块的数据, $y\in\{0,1\}^k$为区块旧数据的哈希值, 即$y=G(s,x)$. 为了扩展区块链$C$到新链$C^\prime:=C||B^\prime$, 新增加的区块$B^\prime:=\langle s^\prime, x^\prime, ctr^\prime, y^\prime\rangle$ 应满足 $s^\prime:=H(ctr,G(s,x),y)$.
修改区块
当采取某种共识机制达成一致时, 用新区块$B_i^\prime$替换$B_i$, 其中$B_i^\prime=\langle s_i,x_i^\prime, ctr_i, y_i\rangle$. 此时新区块$B^\prime_i$的哈希值会改变, 所以$s_{i+1}\neq H(B^\prime_i)$, 使得哈希链被破坏. 但由于$y_i$没有变, $y_i$记录的是旧数据的哈希值, 利用$y_i$可以计算$s_{i+1}=H(ctr, y_i, y_i)$, 所以仍存在一哈希链路保证区块链的完整性.
总结
区块链协议的不可变性是一把双刃剑, 其抗篡改的特性有助于在互不信任的但共同遵守共识机制的参与者之间形成单一的链, 但也在一定程度上限制了区块链但大规模应用. 本文介绍了近几年学术界提出的四种可编辑区块链模型, 并对他们的编辑粒度、可执行的操作进行了分析.
参考文献
- Nakamoto S, Bitcoin A. A peer-to-peer electronic cash system[J]. Bitcoin.–URL: https://bitcoin. org/bitcoin. pdf, 2008, 4.
- 袁勇,王飞跃.区块链理论与方法.北京:清华大学出版社,2019.
- 袁勇,王飞跃.可编辑区块链:模型、技术与方法[J].自动化学报,2020,46(05):831-846.
- G. Ateniese, B. Magri, D. Venturi and E. Andrade, "Redactable Blockchain – or – Rewriting History in Bitcoin and Friends," 2017 IEEE European Symposium on Security and Privacy (EuroS&P), Paris, 2017, pp. 111-126, doi: 10.1109/EuroSP.2017.37.
- H. Krawczyk and T. Rabin. Chameleon signatures. In NDSS, 2000.
- Paul Feldman, "A practical scheme for non-interactive verifiable secret sharing" in Foundations of Computer Science, IEEE, 1987.
- Shamir A.How to share a secret.Communications of the ACM,1979,24(11):612-613.
- Oded Goldreich, "Secure multi-party computation", Manuscript. Preliminary version, vol. 78, 1998.
- K. Ashritha, M. Sindhu and K. V. Lakshmy, "Redactable Blockchain using Enhanced Chameleon Hash Function," 2019 5th International Conference on Advanced Computing & Communication Systems (ICACCS), Coimbatore, India, 2019, pp. 323-328, doi: 10.1109/ICACCS.2019.8728524.
- Ronald L. Rivest, Adi Shamir and Leonard Adleman, "A method for obtaining digital signatures and public-key cryptosystems", Communications of the ACM 21.2, pp. 120-126, 1978.
- 李佩丽,徐海霞,马添军,穆永恒.可更改区块链技术研究[J].密码学报,2018,5(05):501-509.
- V. Buterin, On public and private blockchains, [online] Available: https://blog.ethereum.org/2015/08/07/on-public-and-private-blockchains/.
- K. Petrasic, M. Bornfreund and Beyond Bitcoin, The blockchain revolution in financial services, [online] Available: http://www.whitecase.com/publications/insight/beyond-bitcoin-blockchain-revolution-financial-services.
- Puddu I, Dmitrienko A, Capkun S. µchain: How to forget without hard forks[J]. IACR Cryptology ePrint Archive 2017/106, 2017.
- A. Marsalek and T. Zefferer, "A Correctable Public Blockchain," 2019 18th IEEE International Conference On Trust, Security And Privacy In Computing And Communications/13th IEEE International Conference On Big Data Science And Engineering (TrustCom/BigDataSE), Rotorua, New Zealand, 2019, pp. 554-561, doi: 10.1109/TrustCom/BigDataSE.2019.00080.
- D. Deuber, B. Magri and S. A. K. Thyagarajan, "Redactable Blockchain in the Permissionless Setting," 2019 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 2019, pp. 124-138, doi: 10.1109/SP.2019.00039.
- Politou E, Casino F, Alepis E, et al. Blockchain mutability: Challenges and proposed solutions[J]. IEEE Transactions on Emerging Topics in Computing, 2019.